3 A glimpse at the PSBC model
The monotonicity property we briefly mentioned in the last section means trouble. It is a manifestation of a topological obstruction that a 1D model cannot overcome. For this reason, we have to use a somewhat “bigger”" model, of the form
\[\begin{equation} \begin{split} U^{[n+1]} = U^{[n]} + \Delta_t^{u}\,f(U^{[n]},\alpha^{[n]}),\\ P^{[n+1]} = P^{[n]} + \Delta_t^{p}\,f(P^{[n]},\beta^{[n]}), \end{split}\tag{3.1} \end{equation}\]
where the variable \(P^{[\cdot]}\) will be responsible for fixing the issue. Here the nonlinearity is \(f(u,w):= u(1 - u)(u - w)\) and is the same for both equations, although both variables \(\alpha^{[\cdot]}\) and \(\beta^{[\cdot]}\) are adjusted separately through optimization of a cost function. Many details are given in the paper, to which we refer the reader to.
In essence, this is the heart of the Phase Separation Binary Classifier (PSBC), which is nothing but a new type of Recursivce Neural Network.
What should be added at this point is that the model in fact is a bit bigger than what is seen in (3.1), reading as
\[\begin{equation} \begin{split} \frac{U_{m}^{[n + 1]} - U_{m}^{[n]}}{\Delta_t^u} &:= \frac{\varepsilon^2}{\Delta_x^2}\left( U_{m+ 1}^{[n + 1]} - 2 U_{m}^{[n + 1]} + U_{m- 1}^{[n + 1]} \right) + f(U_m^{[n]};\alpha_m^{[n]} ), \quad \text{for} \quad 1\leq m \leq \mathrm{N_u},\\ \frac{ P_j^{[n+1]} - P_j^{[n]}}{\Delta_t^p} & := f(P_j^{[n]}; \beta_j^{[n]}), \quad \text{for } \quad 1\leq j \leq \mathrm{N_p}, \end{split}\tag{3.2} \end{equation}\]
There are many hyperparameters, which we will refrain from explaining here. In summary, they are not only tied to the dynamics of these equations, but also used for model compression purposes; Section 2 of the paper has a thorough description of their role.
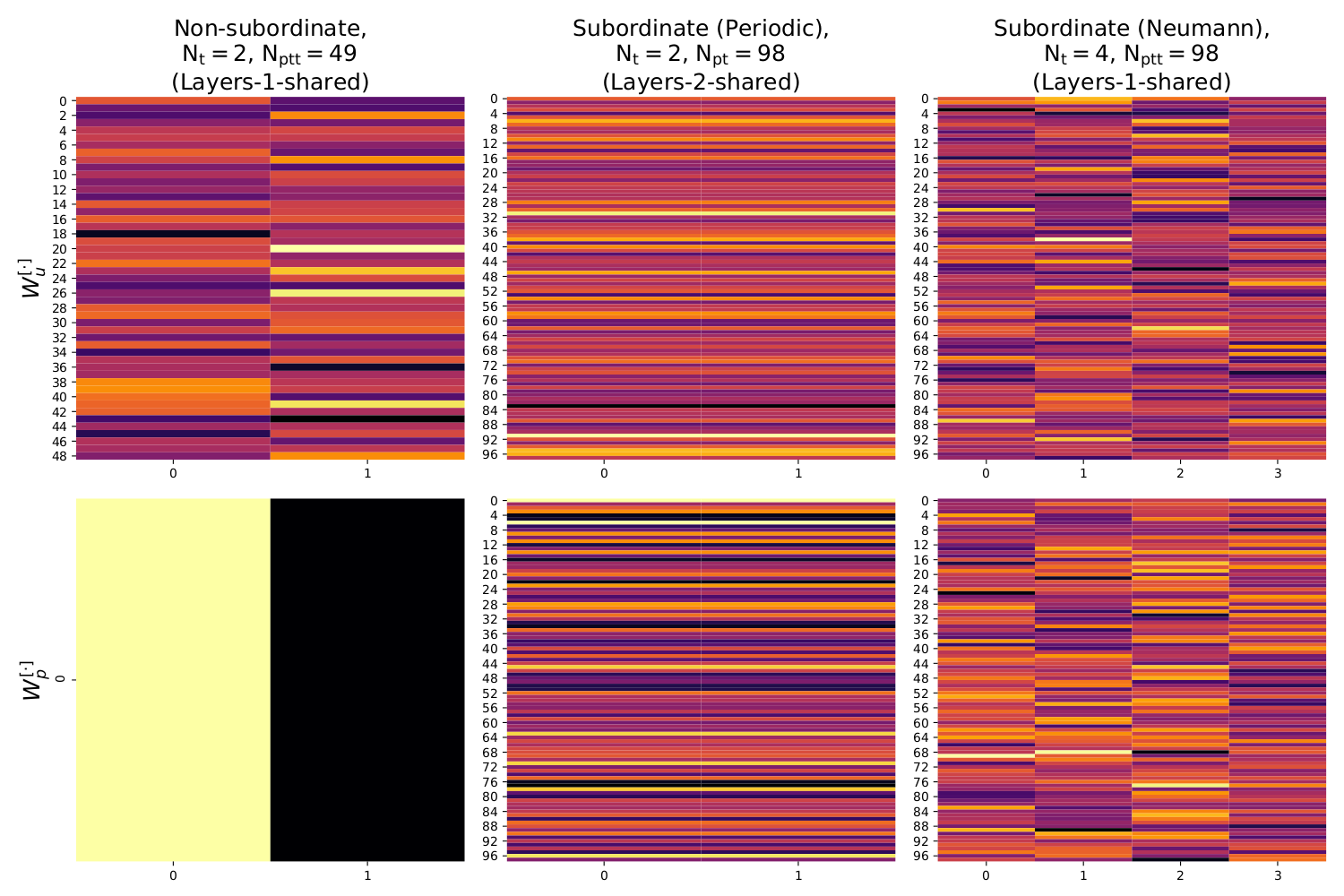
Heatmaps of trainable weights for some trained PSBC models under different architectures. The first row of heatmaps concerns weights associated to \(\alpha^{[\cdot]}s\), whereas lower row concerns weights associated to \(\beta^{[\cdot]}\).
In the next section we will test the PSBC on pairs of digits in the MNIST database.